고정 헤더 영역
상세 컨텐츠
본문
데이터가 표현되는 방식에 대해 배운다
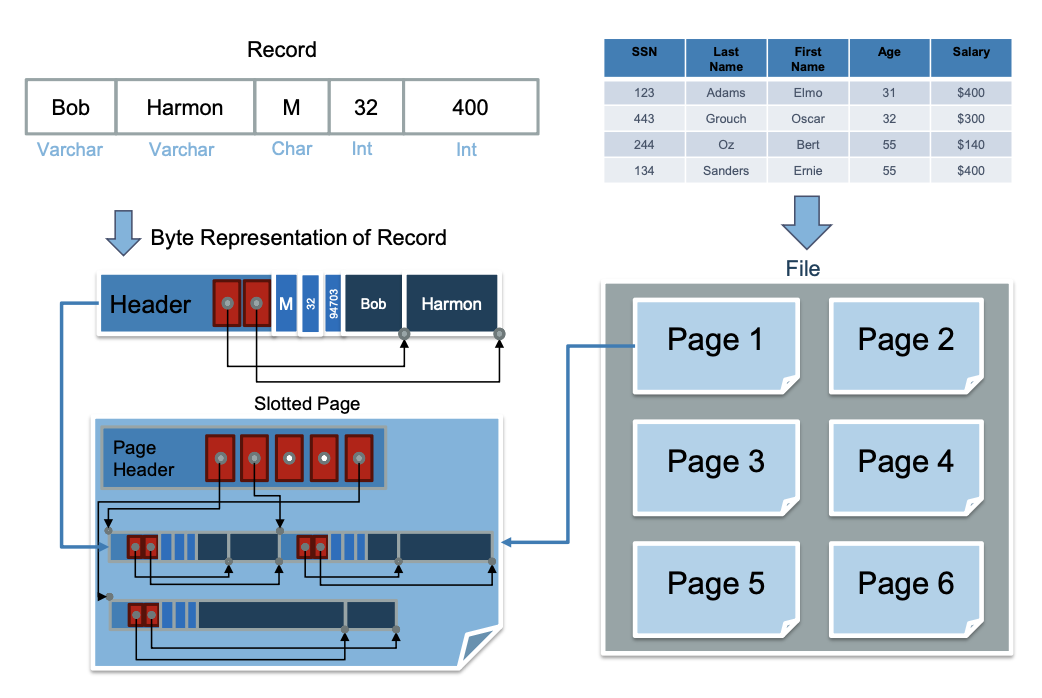
관계형 모델에는 행열로 이루어진 테이블이 존재함
이 테이블들은 파일로 매핑됨 (파일은 디스크의 페이지로 구성되어있음)
각 테이블들은 레코드들로 구성되어 있음
레토드들은 메모리에서 바이트 배열로 표현됨
-> 이 바이트들이 메모리의 페이지에 저장되는것
파일, 페이지, 레코드 순서로 어떻게 디스크에 저장되는지 살펴본다.
Files
테이블은 disk space manager에 의해 논리적 파일로 저장됨
파일안에 여러개의 페이지들이 있고
페이지 안에 여러개의 레코드가 있음
페이지가 disk에 있을 때는 disk space manager의 관리를 받고
페이지가 memory에 있을때는 buffer manager의 관리를 받음
-> DBMS의 더 상위계층의 모듈들은 buffer manager가 저장한 메모리 표현의 페이지를 기반으로 동작한다
DBMS의 상위 계층에서 사용할 수 있는 API에는 레코드의 삽입, 삭제, 수정이 있다.
-> 특정 레코드를 ID로 관리함! (참조 가능한 레코드 ID를 가짐)
-> 즉 이 ID를 포인터라고 생각하면 된다 (레코드가 위치한 페이지ID, 페이지 안에서의 위치 쌍으로 이루어짐)
경우에 따라 데이터베이스 파일은 파일 시스템을 통하지 않고 raw 디스크 장치에 직접 구현될 수 있다.
데이터베이스 안의 파일은 다양한 방식으로 구조화된다.
1. heap file : 레코드가 순서없이 임의로 페이지에 배치됨 -> 모든 레코드를 스캠할 때 적합
2. clustered heap file : 비슷한 값을 가진 레코드와 페이지를 그룹화함 -> 빠른조회, 효율적인 수정
3. sorted files : 정렬된 채로 유지함 -> 특정 수넛로 겁색, 혹은 범위에 맞게 검색할 때 유용
4. index files : B+ tree, Linear hashing -> 데이터를 조회하기 위한 디스크 기반 자료구조 -> 빠른 조회, 효율적인 수정
인덱스 파일은 레코드를 직접 포함하거나, 다른 파일에 있는 레코드를 참조하는 포인터를 포함한다
== 즉 다른 파일의 인덱스를 참조하는 구조를 가질 수 있음!!
Unordered Heap Files
레코드가 순서없이 임의로 저장됨 -> "heap" 자료구조와는 다른거니까 착각하지 말것!!
힙 파일에서는 페이지가 할당/해제된다.
레코드 수준의 작업을 지원하려면
- 파일 내에 있는 페이지
- 비어있는 free 페이지
- 페이지에 담겨있는 레코드
들을 추적할 수 있어야한다!
!! 리스트로 간단히 구현해보자
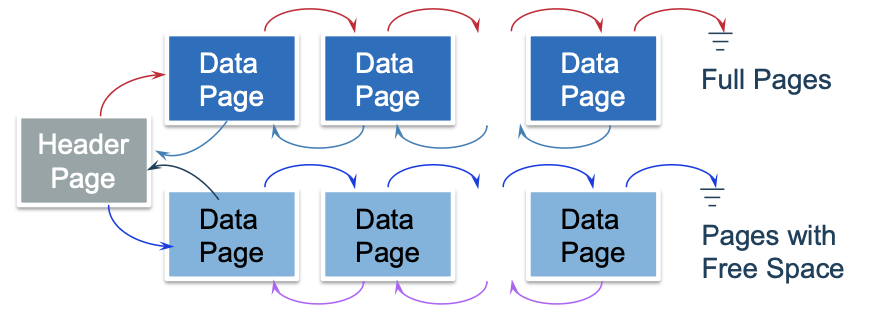
디스크의 어느 공간에 Header Page라는 페이지가 있다.
-> 헤더 페이지의 위치는, 데이터베이스의 catalog에 저장되어 있다. (페이지 ID, heap file 이름)
헤더페이지 안에는 두개의 포인터가 있는데
1. full pages를 연결한 리스트 (삽입공간이 없는 가득찬 페이지를 모아둠)
2. free space pages를 연결한 리스트 (삽입공간이 남아있는 페이지를 모아둠)
두개의 포인터를 포함한다.
각각의 연결리스트는 "이중 연결 리스트" 형태로 생성된다.
단점 : 내가 원하는 사이즈의 빈 공간을 찾을때까지 free space 리스트를 계속 탐색해야한다.
!!Page Directory를 사용하자
헤더파일을 여러개 만들어서 사용하는 방법이다.
이전에는, 헤더파일만으로는 얼만큼의 빈 공간이 있는지 알 수 없었다.
-> 이런 정보를 헤더파일에 넣어버리자!
카탈로그에 저장되어 있는 첫번째 헤더 페이지가 있고, 나머지 헤더페이지들은 연결리스트 형태로 저장된다.
이 헤더페이지들의 모음을 directory라고 한다.
각각의 헤더페이지에는 다른 페이지에 대한 엔트리 (페이지의 자유공간 크기, 포인터)가 저장된다.
-> 헤더페이지를 RAM에 캐시해두면, 접근비용이 낮음!
-> 자유공간을 찾을때도 연결리스트를 타고 가는게 아니라, 헤더페이지의 엔트리를 보고 찾을 수 있다!
Page Layout
페이지를 어떻게 설계할것인지 정해야 한다.
- 헤더영역
페이지에 대한 메타데이터를 저장한다.
레코드 개수, 자유공간 크기, 다음 페이지 포인터, 비트맵, 슬롯 테이블 등등이 포함된다.
설계에 고려해야 할 부분도 있다.
- 레코드의 길이
-> 고정 길이 페이지 (모든 레코드의 길이가 동일함)
-> 가변 길이 페이지 (레코드마다 길이가 다름)
이에 따라 페이지 레이아웃을 다르게 설계해야함!
- 레코드 ID로 레코드를 찾는 방법
-> 레코드 ID는 페이지 ID, 페이지 내 위치로 구성된다.
-> "위치"는 무엇인지, 시간이 지나도 레코드 ID가 안정적으로 유지될 필요가 있음
- 레코드 추가/삭제 방법
등등...
페이지 레이아웃의 옵션은 크게
1. 레코드의 길이 (고정/가변)
2. 페이지 자유공간을 (압축/비압축)
-> 결정에 따라 레이아웃이 달라진다
Indexes
힙파일에서 레코드를 검색할 때...
-> ID를 이용 : 포인터와 같으므로 빠르게 찾을 수 있음
-> 값 기반 검색 : 모든 레코드를 순차적으로 스캔해야 하므로 비효율적임
이런 문제점을 해결해주는게 인덱스이다! 특정 속성을 기준으로 데이터를 찾을 수 있도록 설계된 데이터 구조이다.
Fixed Length Records
레코드의 길이가 고정되어 있을 때 (옵션1)
압축/비압축 일 때 페이지 레이아웃이 어떻게 달라지는지를 살펴본다 (옵션2)
Packed
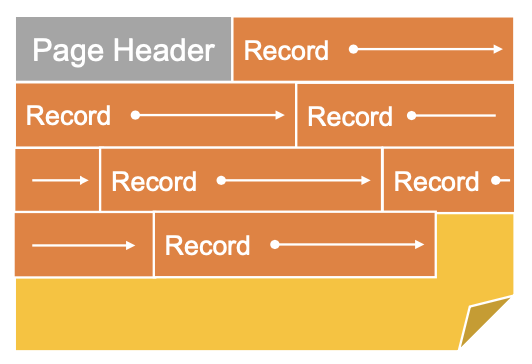
페이지에 레코드를 저장할 때 빈공간 없이 꽉꽉 채우는 방법이다!
각 레코드 ID에는 페이지ID, 페이지 내 위치가 저장된다.
모든 레코드의 길이가 같고, 사이에 빈공간이 없으므로 단순히 offset으로 이용하면 된다!
=> 즉 단순 산술연산으로 해결이 가능하다.
(4번째 레코드의 시작위치를 알고싶으면, 페이지 헤더 크기 + (3 * 레코드길이) 로 간다히 알 수 있다)
- 레코드 삽입
헤더에 있는 현재 레코드 수만 알면, 단순 산술연산으로 비어있는 페이지 위치를 알 수 있다!
즉 삽입할 때 그냥 맨 뒤에 추가해주면 된다.
- 레코드 삭제
삭제가 조금 복잡하다. 중간에 있는 레코드를 삭제하면, 빈공간을 채우기 위해 뒤에 있는 레코드들을 앞으로 한칸씩 땡겨온다.
그러면 레코드들의 offset이 바뀌므로, 레코드 ID도 변경해줘야 한다.
=> 이걸 업데이트 하는게 cost가 크다!
Unpacked

사이에 빈공간이 있어도 괜찮다! -> empty page는 bitmap을 헤더에 추가해서 해결한다.
단순히 비트맵을 채우는것만으로 비어있는지 여부를 알 수 있다 (이 경우 빨간색이면 차있는거, 파란색이면 비어있는거)
레코드ID에서도, offst이 아니라 몇번째 slot인지만 저장해주면 된다.
- 레코드 삽입
비트맵에서 빈 레코드를 찾아서 채워준다. 비트맵을 채워져있음으로 수정한다.
- 레코드 삭제
단순히 비트맵을 토글하는것만으로 삭제할 수 있다. unpacked이므로 다른 레코드를 옮겨줄 필요도 없다
즉 레코드ID가 변하지 않는다!
결론 : 고정길이 레코드면 unpacked 레이아웃이 더 나은 선택일 수 있다.
(비트맵만큼의 공간이 필요하지만, 삭제할때마다 업데이트 비용이 더큼)
Variable Length Records
-> 레코드마다 길이가 다른 경우 (문자열 같은 상황,.,,?)
문제점 : 각 레코드가 어디에서 시작하고 끝나는지 파악하기 어렵다 (다 따로 노니까)
레코드 추가, 삭제할때도 문제가 생긴다! (빈공간이 추가하려는 레코드보다 작으면, 더 큰 빈공간을 찾아야함)
Footer, Slotted page
페이지의 메타데이터를 헤더가 아닌, footer에 저장한다 (페이지의 맨 마지막에!)
그리고 푸터에 slot directory라는 종류의 메타데이터를 추가한다.
-> 이 때 슬롯디렉토리는 "오른쪽에서 왼쪽으로" 증가한다는점 주의할것! (맨 마지막부터 커짐)
- 첫번째 공간 : 자유공간을 가리키는 포인터
- 나머지 공간 : 채워진 레코드의 길이, 포인터(오프셋) 쌍
-> 오프셋은 페이지 시작점부터 레코드가 시작하는 위치까지의 바이트수로 표현됨
-> 이 정보들로 레코드의 "시작(포인터)"과 "끝(포인터+오프셋)"을 결정함
레코드 ID는, 슬롯 디렉토리에서의 위치가 저장된다 (이때 시작이 제일 오른쪽인것 주의)

이런 페이지가 있다고 하면... -> 레코드 아이디에 저장된 오프셋이 "4"이면,
슬롯 디렉토리의 4번째 정보 (12가 저장된곳)의 레코드라는 의미이다.
해당 슬롯에있는 포인터 (초록색 선)와 레코드 길이(12)로 레코드에 접근한다!
- 삭제 : 해당 슬롯 디렉토리의 포인터, 항목을 null로 설정함 (길이와 포인터를)
-> 다른 레코드ID에 영향을 안준다!
-> 삭제된 공간은 이제 사용되지 않는 상태가 된다. (free space가 된것)
- 삽입 : 자유공간에 추가한다.
1. 자유공간을 확인 -> 자유공간 포인터가 가리키는 페이지의 끝 부분에 삽입한다.
2. 슬롯에 정보 저장하기 -> 추가한 레코드의 포인터와 길이를 슬롯이 저장해둔다. 기존 자유공간 포인터를 활용해준다.
이 때....
a. 새로운 슬롯 만들기 : 슬롯배열의 마지막에 새로운 슬롯을 추가한다.
b. 슬롯 재사용 : 삭제때문에 null이 됐던 슬롯을 재사용한다.
3. 자유공간 포인터를 업데이트한다.
free space framentation
삭제된 레코드가 저장되어 있던 공간은, 재사용 되지 못하고 계속 남아있다 (슬롯만 재사용 되는것!)
-> 위에 빈공간이 뻥뻥 뚫려 있는데, 맨 마지막에 빈공간이 부족해서 큰 레코드를 담지 못하는 상황이 올수도 있다!
이를 위해 자유공간들을 병합하기 위해, 페이지의 데이터를 재구성해준다.
=> 앞으로 땡기면서 (압축하면서) 하나로 모으고, 각 레코드의 포인터를 업데이트해준다.
이 때, 각 슬롯들의 포인터만 업데이트 하면 되어서 레코드ID자체에는 변화가 없다.
즉 사용자들 입장에서는 달라질게 없으므로 매우 안정적인 방법임!
페이지 재구성은 언제 해야할까?
- eager : 적극적 방식. 삭제가 생길때마다 재구성함
- lazy : 게으른 방식, 자유공간이 부족할때까지 재구성을 미룸
=> lazy방식을 사용하는것이 이득일 수 있음 (삭제 후 삽입이 별로 없으면 자유공간이 부족할 상황 자체가 안생길 수 있기 때문임)
Growing Slots
슬롯이 부족한 상황에서는 어떻게 해야할까.. -> 그냥 추가해주면 된다!
그리고 이 상황에서 footer를 사용하는 설계가 유용하다. (슬롯 개수를 같이 저장해준다)
| 레코드 시작 -> 방향으로 자람 | --> | --> |
| ((비어있음)) | ||
| <--- | <--- | |
| <- 방향으로 자람, 슬롯 시작 | 자유공간 포인터 | 슬롯개수 저장 |
대충 페이지를 이렇게 생각해보면.. 레코드도 비어있는 방향으로 자라고, 슬롯도 비어있는 방향으로 자란다.
=> 즉 마지막 레코드랑, 마지막 슬롯이 만나는 순간에는 그냥 페이지에 빈공간이 없다는뜻!!
슬롯 개수는 null을 포함한 전체 슬롯 개수라는점에 유의하자! 슬롯개수를 저장하는 이유는,, 슬롯의 마지막 포인터마냥 사용하려는것같다 (슬롯 자체는 데이터 길이가 고정적이니까)
slotted page 장점
재구성이 편하다는 점에서 유용하다. (레코드 ID를 업데이트할필요가 없음)
특히 null필드가 있을 때 고정길이 레코드라고 해도 레코드의 길이가 짦아진다
-> 고정길이 레코드에도 slotte page를 사용하는것이 좋을 수 있다!
Record LAYOUT
레코드 내의 필드를 어떻게 표현할것인가?
관계형 모델에서 각 레코드는 고정된 타입을 가진다.이 정보가 스키마로 시스템 카탈로그에 별도로 저장된다.
(즉 레코드 각각에 타입을 저장할 필요가 없음)
레코드 포멧에서의 목표는 메모리와 디스크에서 레코드를 압축하는것이다 (데이터를 가능한 작게 유지해서 I/O효율을 높이고, 개별 필드를 빠르게 조회할 수 있도록 해줌)
* 데이터베이스 시스템은 디스크에 데이터를 저장할 때 메모리의 형식을 그대로 저장한다. (디스크에 저장되는 바이트 표현은 메모리와 정확히 동일함!)
System Catalog
데이터베이스 내부에서 사용하는 메타데이터 저장소
-> 데이터 베이스의 구조, 구성요소, 제약조건 등등을 저장함
- Relation 정보 : 테이블 이름, 파일 위치, 파일 구조, 속성(attribute)
- Index 정보 : 인덱스 이름, 인덱스 자료구조 (B+트리인지 등등) 검색키
- 무결성 제약 : 키 제약, 참조 제약, 도메인 제약
- View : 뷰 이름, 뷰 정의
- 성능과 관련된 정보 : 통계 (데이터 분포), 권한 (사용자의 역할), buffer pool size
* 카탈로그 자체가 테이블(relation)으로 저장된다.
Fixed Length
필드들의 사이즈가 고정되어 있는것
-> 각 필드의 사이즈는 스키마를 통해 알 수 있으므로, 단순히 산술연산만으로 알 수 있다.
예를 들어, 필드 I를 찾고싶으면 I - 1필드의 길이합을 오프셋 삼아서 찾으면 된다.
문제점 : NULL값이 있을 때 공간이 낭비된다. (null인 필드도 그만큼의 공간을 띄워두니까)
Variable Length
가변길이 -> 사이즈가 매번 달라지는 필드 (string을 생각해보자!)
- 방법1 : 크게 저장하기 (padding)
-> 고정된 큰 길이로 전부다 할당해준다. (3바이트만 필요한 데이터도 그냥 32바이트 차지하게)
문제점 : 할당된 공간보다 큰 데이터가 들어오면 문제가 생긴다.
- 방법2 : 구분자 활용하기 (, 활용)
-> CSV파일처럼, 각 필드 사이에 쉼표를 넣어서 다른 필드라고 명시해준다
특정 필드를 가져오려면, 쉼표를 하나씩 세면서 필드에 도달해야함
문제점1 : 구분자로 사용하는 문자가 데이터 내부에 포함될 수 있음
-> 이스케이프 문자를 사용한다고 해도, 이건 공간낭비임!
문제점2 : 성능 문제, 특정 필드 접근을 위해 메모리 스캔을 많이해야함
- 방법3 : 레코드 헤더 도입

-> 가변길이 필드를 모두 레코드의 끝으로 이동시키고, 레코드 헤더에 가변길이 필드를 가리키는 포인터를 저장함
이렇게 하면 고정길이는 위에 있는 방식처럼 접근하고 (오프셋으로) 가변길이는 포인터로 접근하면 된다!
NULL값 처리도 단순히 다음 포인터와 동일한 위치를 가리키도록 하는것으로 해결가능하다
정리

1. 논리적 구조인 "테이블" (오른쪽 위)
2. 테이블을 페이지로 가득 찬 파일로 매핑함
3. 각각의 페이지에는 여러개의 레코드들이 저장됨 -> 슬롯 페이지 구조 등등,,
4. 레코드를 다중 필드가 포함된 바이트 표현으로 매핑하는 방법
Cost Model And Analysis
다양한 종류의 파일 구조 중, 어떤것을 선택하는것이 가장 좋은지 찾는것
-> 처리중인 액세스 패턴에 따라 다름!
-> 정량적인 trade off를 측정한다 (추후 쿼리 최적화와 관련됨)
Cost Model
비용모델의 변수를 확인한다.
- B : 파일에 있는 데이터 블록의 개수
- R : 블록 당 레코드 개수 (이 떄 모든 블록에서 R이 같다고 가정함(
- D " 디스크 블록을 읽고 쓰는데 걸리는 평균시간 (단일값으로 평균만 사용)
* 순차접근과 랜던접근을 구분하지 않음
* 프리페칭, I/O 계층이 요청을 예측하여 데이터를 미리 가져오지 "않는다고" 가정
* 메모리 "내부'의 작업비용 무시 (디스크에 접근하지 않으면, 비용이 들지 않는다고 가정)
* 모든 삽입 및 삭제가 "단일 레코드"에만 적용된다고 가정
* equality selaction에서는 정확히 "하나"의 일치항목만 있음을 가정함 (where cllumn = value 같은것)
* HEap 파일의 경우, 삽입은 항상 파일의 끝에만 추가된다고 가정
* sorted 파일의 경우 항상 압축된 상태로 유지됨
* sorted 파일의 역우 삭제 후 파일을 항상 압축하여 중간에 공백이 없도록 유지한다고 가정
* sorted 파일은 특정 키/특정 열을 기준으로 정렬된 수 있음
Heap Files VS Sorted Files
heap file과 sorted file을 비교해본다

다음과 같이 하나의 INTEGER 열만 존재하는 데이터베이스를 생각해보자.
B = 5 (블록개수) R = 2(레코드수) D = 5ms(디스크 블록 접근 시간) 라고 가정하자.
Scan ALL Records
전체 레코드를 스캔한다. 이 경우 그냥 데이터베이스의 앞에서부터 하나씩 읽으면 되므로
Heap fiel과 Sorted file에서의 차이가 없다.
즉 모든 블록을 그냥 순서대로 읽으니까 B * D = 5 + 5 = 25ms 가 나온다.
Equality Search
WHERE column = value 형식의 쿼리에 일치하는 특정 레코드를 찾는 작업
-> 지금 과정에서는 "조건에 맞는 레코드가 한개만 존재" 한다는 가정을 하는것에 주의!
=> 일치하는 레코드가 0개일 때, n개일 때 등등을 고려하지 않는다 (이걸 고려하면 좀 더 복잡해짐!)
- Heap file
정렬이 안되어 있으므로 그냥 왼쪽부터 하나씩 확인해 나가는 방법밖에 없음
일치하는게 딱 "한개"만 있다고 가정하므로, 일치하는 레코드를 찾으면 즉시 중단이 가능함!
! B개의 페이지 중 특정 페이지에 키가 있을 확률은 1/B이다.
! 키가 페이지 I에 있으면,, 총 I개의 페이지에 접근한다
-> 기대값을 구하려면? 확률 * 접근비용 으로 계산한다
-> "개수"에 대한 기대값이므로, 접근비용은 I를 사용한다.

결론 : 디스크 접근 비용 D를 추가해주면 $\frac{2}{b} \cdot D$라고 생각하면 된다!
- Sorted File
이진탐색을 이용한다! (정렬되어있다는 점을 최대한 이용하기)
! binary search의 시간복잡도는 worst에서 logB이다.
-> 우리가 찾고자 하는것은 기대값 (Average) 이므로.. 힙파일에서 했던것과 비슷한걸 해야한다!
-> "확률 * 접근비용" 을 위해 확률과 접근비용이 무엇인지 생각해보자

이진탐색이므로,,, 처음 시작에서 양쪽으로 점점 이동한다.
-> 첫번재 mid가 될 수 있는건 1개
-> 그 다음 두번째 mid가 될 수 있는건 2개 (첫번째의 양쪽)
-> 세번째는 4개
... 이런식으로 몇번째 접근인지에 따라 도달할 수 있는 페이지의 개수가 변한다!
이걸 고려하면..
첫번째에 찾을 수 있는 확률은 $\frac{1}{B}$, 두번째에 찾을 수 있는 확률은 $\frac{2}{B}$ ... 이런식으로 생각할 수 있다.
그리고 접근비용 또한 몇번의 I/O가 필요한지 니까 첫번째에는 1, 두번째에는2, 세번째에는 3.. 순으로 증가한다.

결론 : 디스크 접근 비용 D를 고려해주면 $\log_2 B \cdot D$ 가 된다.
Range Search
범위검색! (3 ~ 7 사이의 모든 값을 찾는 문제)
- heap file
전체탐색을 진행해야 한다! (정확히 범위안에 포함되는 레코드가 몇개인지 추측이 불가능함)
-> 전체탐색 시간과 동일하다 = $B \cdot D$
- sorted file
범위의 시작을 이진탐색으로 찾는다 (equality search와 같음)
그리고 범위의 마지막까지 순서대로 탐색한다 (그냥 모든 페이지를 하나씩)
=> 시작점 찾는 시간 + 범위에 포함되는 페이지를 완전탐색하는 시간
=> $\log_2 B \cdot D + pages \cdot D$
Insert
레코드 추가할 때
- heap file
힙파일은 그냥 맨 뒤에 추가해준다! 파일의 끝 페이지는 계산을 통해 직접 접근할 수 있다고 가정하면 (즉 디스크 I/O가 필요없음)
단순히 맨 뒤에 레코드를 삽입하기 위한 동작만 고려하면 된다.
이 떄 디스크의 정보를 수정할때는 디스크에 바로 쓰는게 아니라 메모리로 올린 다음에 처리해야 한다는 점을 고려하면...
디스크에서 해당하는 페이지를 메모리로 올릴 때 D, 메모리에서 수정한 페이지를 다시 디스크로 내릴 때 D
총 $2 \cdot D$ 의 비용이 든다
- sorted file
순서에 맞춰서 파일의 "중간에" 작성해야 한다.
일단 새로운 레코드가 들어갈 위치를 찾기위해 이진탐색을 이용한다 (equality serch = $\log_2 B \cdot D$)
파일이 중간에 들어가면, 그보다 큰 데이터들 (오른쪽에 있어야 하는애들)을 오른쪽으로 밀어줘야 한다.
즉... 파일의 나머지 부분을 전부 훑으면서 I/O를 발생해야 한다.
평균적으로 삽입은 파일의 중간에서 이루어지기 때문에...... -> 옮기기 위해 평균적으로 파일의 절반을 I/O해야한다
옮기는 비용은 힙 파일에서 읽고 쓰기 비용 (2D) * 파일의 절만 (2/B)이므로 총 $B \cdot D$ 이다.
결론 : $\log_2 B \cdot D + B \cdot D $
Delete
-heap file
일단 삭제할 레코드를 찾는다 ( $\frac{2}{b}$) <- 여기에는 해당 페이지를 메모리로 올리는것도 포함됨!
메모리로 올린 페이지를 수정하고 (레코드를 삭제하고) 다시 디스크로 내려준다 (1)
결론 : $(\frac{2}{b} + 1) \cdot D$
근데... 힙파일은 구멍 신경 안쓰는걸까..?
- sorted file
삭제할 레코드를 찾는다( 이진탐색 $\log_2 B$) <- 해당 페이지를 메모리로 올리는것도 포함
근데.... sorted에서는 파일이 packed상태라고 가정했기 떄문에 빈 공간을 채우기 위해 오른쪾에 있는 있는 데이터를 전부 왼쪽으로 한칸이도 시켜줄 필요가 있다! (위에서 계산한것처럼 B가 또 필요함)
결론 : $\log_2 B \cdot D + B \cdot D $
| Heap File | Sorted File | |
| Scan all records | $B \cdot D$ | $B \cdot D$ |
| Equality Search | $\frac{2}{b} \cdot D$ | $\log_2 B \cdot D$ |
| Range Serch | $B \cdot D$ | $\log_2 B \cdot D + pages \cdot D$ |
| Insert | $2 \cdot D$ | $\log_2 B \cdot D + B \cdot D $ |
| Delete | $(\frac{2}{b} + 1) \cdot D$ | $\log_2 B \cdot D + B \cdot D $ |
=> 삽입과 삭제를 비교했을 때 heap file과 sorted file의 차이를 잘 보자!
(heap file은 삽입은 빠르고, 삭제는 느림 sorted file은 둘 다 같음)
=> INDEX를 도입하면 더 빨라진다고 한다..!
'학교 > 데이터베이스시스템응용' 카테고리의 다른 글
| 14. 10장 : TREE-STRUCTURED INDEXING (1) (0) | 2024.11.25 |
|---|---|
| 13. 9장 : STORING DATA - DISKS AND FILES (3) (0) | 2024.11.25 |
| 11. 9장 : STORING DATA - DISKS AND FILES (1) | 2024.11.21 |
| 10. 5장 SQL: QUERIES,CONSTRNNTS, TRIGGERS - SQL 연습하기 (0) | 2024.10.17 |
| 9. 5장 SQL: QUERIES,CONSTRNNTS, TRIGGERS - VIEW, subqueries, WITH, NULL (2) | 2024.10.16 |




