고정 헤더 영역
상세 컨텐츠
본문
파일에서 데이터를 레코드ID가 아닌, 값으로 탐색하고 싶다
-> 앞에 나온 힙파일 검색방법 처럼,, 냅다 모든 데이터를 탐색하는것은 오래걸ㄹ
-> index를 도입하자!
RAM내에서의 자료구조 (이진트리, AVL, Red-Black tree, hash table) 등등이 있었음...
-> 디스크 기반의 자료구조 (페이지 단위로 구성된 자료구조)
Index
인덱스란 : search key를 통해 데이터를 빠르게 조회하고 수정할 수 있게 해주는 자료구조
- Lookup : 조회! 생성되 인덱스의 종류에 따라 다를 수 있음. 다양한 연산을 지원함 (equality, 1-d range, 2-d region)
- Search key : 관계형 모델에서는 테이블의 컬럼의 부분집합을 결합해 키를 구성한.
-> 반드시 고유할 필요는 없음!
-> 하나의 컬럼이 될 수도 있고, 여러개의 컬럼의 조합으로 검색할수도 있음
- Data Entries : 인덱스에 저장된 데이터
인덱스 종류에 따라 달라짐 (수업시간에는 인덱스에 key, record ID가 저장된다고 가정)
-> 레코드 ID는 힙파일속 레코드를 가리키는 포인터라고 생각하기
- Manay types : B+ trees, R-Trees, GiST 등등.. 다양한 종류의 인덱스가 존재
=> 아무튼 전부다 "삽입" "삭제" 도 빠르게 지원해야 한다.

이렇게 생긴 sorted file을 생각해보자. (삽입을 위한 공간을 약간 남겨둠)
-> 여기서 그냥 이진탐색을 진행하면 어떻게될까?
레코드가 저장된 파일에서 이진탐색을 진행하면, 이진 트리는 파일에 생성된다
즉 이진트리의 깊이가 깊어질수록 디스크에 접근하는 I/O는 많아지게된다.
그리고 저장하는 레코드의 크기와, serch key의 크기에 차이가 클 수 있다/
하나의 레코드 사이즈가 100인데, search key로 사용하는 attribute는 한개뿐일 수 있다.
=> 즉 파일에 대한 "검색 파일"을 구축하자는 아이디어가 있다!
search key와 페이지 ID로만 구성되는 파일을 구성한다.
페이지 ID로 가므로, 하나의 페이지에서 최소값만들 가지고 구성한다.

이렇게.. 각각의 페이지로 갈 수 있는 검색파일을 구축한다.
검색파일또한 "파일"구조 안에 들어가므로 또 페이지단위로 나눠서 생각해보면.....

이런 검색파일이 만들어진다! 즉 더 작은 크기의 파일에서 이진검색을 할 수 있으므로 이득이 생긴다.
이걸 재귀적으로 수행하면.. 검색파일을 위한 검색파일을 또 만들수가 있다

재귀적으로 반복하면...최종적으로 한개의 페이지에 다 담길 수 있는 크기만큼 검색파일을 줄일 수 있다.
중요한점음,, 특정 키를 기준으로 작은건 왼쪽, 같거나큰건 오른쪽 이라는 조건을 만족해야 한다는점이다!
그리고 이걸 위에 큭정 키 양쪽으로 포인터가 존재해야한다.
=> fan out(팬아웃)이 클수록 깊이가 얕아져서 효율성이 높아진다..!
== high fan out인 search tree를 만들어야함
* high fan out 이란? : 트리 기반 인덱스에서 자식노드의 개수가 많다는 뜻 (fan out이 자식노드의 최대개수)
=> fan out이 높으면 당연히 트리 전체의 높이도 낮아짐!
Search
검색할때는 어떻게할까? root 인덱스 페이지부터 시작해서,,, 이진탐색을 진행하면서 내려간다!
leaf 레벨에 도달할때까지 반복하고, 맨 아래 heap file에서 우리가 찾는 레코드를 포함한 페이지를 얻게된다.
=> 복잡도는 $O(\log_F N)$가 된다. (이게 트리의 높이가 되는것!)
( F는 fan-out, N은 원본 파일 페이지 개수)
* 각 노드내에서 또 이진탐색을 진행한다는점을 고려해서 전체 search time을 구한다면....
(각 노드내부에서 이진탐색을 진행하는건 $O(\log F)$)
=> $O(\log_F N \cdot \log F)$
ISAM
Indexed Sequential Access Method
트리를 보면.. 제일 왼쪽에 있는 key는 필요가 없다 (어짜피 최소값이니까)
=> 없애준다! (공간을 절약할 수 있음)
그리고 트리의 모든 레이어를 단일파일로 저장한다
leaf 레벨, 데이터 페이지가 먼저 들어가고 그 뒤에 루트순서대로 인덱스 페이지가 들어간다.
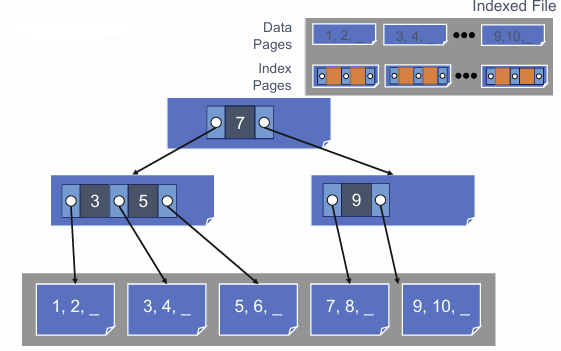
* 데이터가 파일의 앞부분에 연속적으로 배치되어 있으므로 빠른 순차스캔을 지원한다.
but.. 삽입은 약간 힘들다!
페이지에 미리 만들어둔 빈 공간에 들어갈 수 있는 상황이면 단순히 페이지 안에 추가하는것만으로 해결이 가능하다.
하지만... 그러지 못한 상황이면?
=> overflow 페이지가 추가되면서 파일이 확장된다!
그리고 각 인덱스 페이지에 오버플로 페이지를 위한 포인터를 저장해준다.
이런오버플로 페이지는 오버플로 영역에서 페이지들을 "연결리스트" 형태로 관리한다
=> 만약 값이 점점 커지는 상황이면.... 연결리스트 형태의 오버플로 페이지가 파일의 대부분을 차지할 수 있게된다.
=> 연결리스트이므로, 검색할 때 단순 선형검색만 가능하다 == 즉 인덱스가 없는 힙파일과 다름없어짐!!
결론 : ISAM 은 삽입/삭제가 자주 일어나지 않는 데이터베이스에는 적절하지만, 삽입이 자주 일어나면 성능저하가 일어난다.
B+ Tree
ISAM과 매우 비슷하지만, 삽입이 원활하게 이루어진다 (동적 자료구조이기 때문)

* occupancy invariant : 점유 불변 조건, 각 노드의 점유율(채워져 있는 정도)가 해당 노드의 최소 절반이어야함
(루트노드는 예외! 트리가 아무리 커져도 루트노드는 "한개뿐"이다!)
즉 occupancy invariant를 D라고 결정해두었으면, 각 노드의 항목 수는 최소 D이상, 최대 2D 이하여야 한다.
* D를 "차수"라고 한다.
-> 이 상황에서 팬아웃은..? 2D + 1이 된다! (멘 왼쪽 key를 없애고 포인터만 냅둠)
ISAM과 가장 큰 차이점은 트리의 leaf 노드를 순서대로 디스크에 저장할 필요가 없다는점이다.
대신 완전탐색을 지원하기 위해 leaf 노드끼리 (즉 leaf 페이지끼리) 포인터를 이용해 연결리스트처럼 연결되어있다.
이러는 이유는,, 동적 자료구조이기 떄문이다. 나중에 삽입때문에 새로운 데이터 페이지가 필요하게 되면, 연결된 페이지들이랑 멀리 떨어진곳에 페이지를 할당해야 할 수 있다.
B+ tree의 크기
차수, 높이, 팬아웃만 있으면 알아낼 수 있다!
만약.. D = 2, 높이가 1이면 => 팬아웃은 5가된다.
루트 하나와 리프노드 5개(이게 데이터페이지)로 이루어져 있고, 각 리프노드는 4개의 레코드를 저장하므로
총 20개의 레코드를 저장할 수 있다!
비슷하게 D=2, 높이 = 3인 B+트리의 크기는 어떻게 계산할까?
루트노드에 팬아웃이 5개 (자식이 5개)
각각의 자식마다 또 팬아웃이 5개 (각각의 자식이 5개)
또 이 자식들에 팬아웃이 5개 (각각의 자식이 5개)
그리고 이 자식들이 곧 리프노드가 되므로... (리프노드에 레코드는 4개)
5 * 5 * 5 * 4 = 500 개의 레코드를 저장할 수 있다.
일반적으로 128킬로바이트 페이지에서 B+ 트리의 차수는 1600이다.
또 삽입/삭제가 빈번히 일어난 B+트리는 보통 2/3 (67%) 정도만 채워져있다
=> 평균적인 팬아웃은 ((1600 * 2 + 1) * 2) / 3 = 2144가 된다.
128 Kbytes페이지에 레코드 하나의 크기가 40Bytes라고 가정하면..
페이지 하나에 레코드가 총 3200개, 67%라고 생각하면 페이지 하나에 레코드가 약 2144개 들어간다
즉 레벨이 1이면 2144^2개의 레코드 = 4,596,736개
레벨이 2면 2144^3 개의 레코드 = 9,885,401,984개
거의 10억개의 레코드를 저장할 수 있다!!
=> B+트리는 매우 낮은 높이로도 엄청난 양의 레코드를 저장할 수 있다.
또 높이가 매우 낮기 때문에 매우 큰 파일에서 leaf까지 접근하는데 있어서 매우 효율적이다.
Search
ISAM과 같다!!
이진탐색 하듯이 범위에 맞춰서 트리를 타고타고 내려가고, leaf에 있는 레코드 ID를 이용해 레코드에 접근한다.
Insert
leaf node에 빈 공간이 있으면, 그냥 페이지 내부만 수정해주면 된다.
하지만... 꽉 차서 새로운 페이지를 할당해줘야 하는 상황에서 ISAM과 다르다!

이런 상황에서 8을 추가한다고 생각해보자.
제일 왼쪽에 있는 페이지에 추가히야 하지만 페이지에 빈공간이 없다.
=> 8을 삽입할 공간을 만들기 위해 노드를 분할한다!
[2, 3, 5, 7, 8] 을 두개의 페이지에 나눠서 넣는다.
낮은 값 2개는 기존 노드에, 큰 값 3개는 새로운 노드에 할당해준다
...-> 즉 [2, 3] [5, 7, 8] 로 분할해준다.
* 새로 할당한 노드에 더 큰 개수를 넣어주는건 앞으로유지해야 하는 규칙임!
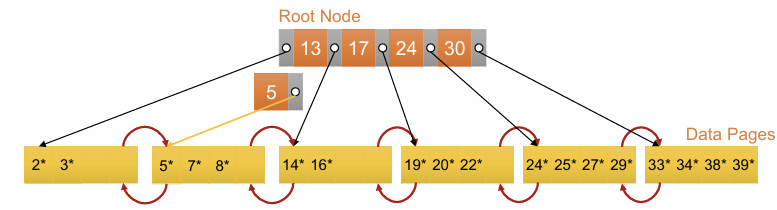
이번에는 새로 할당한 노드 (대표 key로 노드 내 최소값인 5를 사용하는 페이지)의 포인터를 root노드에 추가해줘야 한다.
근데.. 루트노드도 꽉차있다! => 노드 분할!!! (재귀적으로 분할된다)
[5, 13, 17, 24, 30] 을 두개의 페이지로 나눠서 넣는다.
=> [5, 13] [17, 24, 30] 두개의 노드로 분할된다.
root 노드는 1개여야 하기 때문에, 이 위레벨에 올라갈 root노드를 새롭게 만들어준다.
=> 오른쪽 노드에 있는 [17]을 root 노드로 "올려준다!"
* 복사가 아니라 이동이라는 점 주의

최종적으로 이런 모양이 완성된다. 레벨이 1 증가한것을 알 수 있다.
* 주의할점
- leaf 노드에서 분할이 생길 때 : key를 위로 "복사" 한다 (모든 데이터항목이 leaf에 유지됨)
- 내부 노드에서 분할이 생길 떄 : key를 위로 "이동" 한다 (자식노드에는 필요가 없음)
모든 작업을 수행한 후, 트리가 옮바른지 확인하기 위해 불변조건을 점검한다,
1. (ISAM과 같이) 특정 key 기준으로 오른쪽에 있는 모든 key값들이 "이상"이아야함
2. occupancy 조건 : 모든 노드들이 절반이상 채워져 있음
* 루트를 분할해야 하는 상황에서, 트리가 성장한다 (높이가 증가함)
-> 트리가 루트바향으로 성장한다
* 내부 노드만 분할하면, 가로로 넓어짐
* 루트에서 리프까지의 모든 경로는 항상 "같은 길이"를 유지한다. (로그 검색 기능 보장)
delete
노드에서 가장 왼쪽값을 삭제할 때..
-> 부모 노드의 항목을 새로운 왼쪽값에 맞게 업데이트 해야할 까?
업데이트 할 수도 있지만, 실제로는 불필요한 작업이다!
항목을 삭제했는데, 해당 노드에 남은 엔트리 개수가 D 미만일때는 어떻게 해야할까?
=> occupancy 조건을 만족하기 위해 재분배, 병합을 시도해야 한다!
1. 재분배 시도 : 부모노드를 공유하는 인접한 노드에서 엔트리를 가져온다
여기서 성공하면, 추가작업은 필요없다
2. 병합 : 재분배가 실패하면, 형제노드와 병합한다!
-> 두 노드가 하나로 합쳐지므로, 부모노드에서 둘 중 하나를 가르키는 엔트리를 삭제해야 한다
* 병합으로 부모노드의 엔트리가 삭제됐는데, 또 최소개수를 못넘기면 재귀적으로 재분배/병합 과정이 이루어진다.
* 특히 병합의 결과로 루트노드의 모든 엔트리가 삭제되면, 루트노드는 삭제되고 트리의 높이는 감소한다. 병합된 노드가 루트가 된다.
* 실제 구현에서는 occupancy 조건을 엄격하게 지키지 않는 경우도 있다.
=> 재분배/병합 은 비용이 너무 크기떄문에, 페이지가 완전히 비었을때만 트리에서 제거하는 등으로 관리한다.
* 트리의 높이에는 영향이 적기때문에 검색속도가 느려지지는 않지만, 공간낭비가 생길 수 있다.
BULK Loading
대량의 데이터를 한번에 삽입하는 상황
insert를 냅다 반복하기
-> 삽입하는 모든 튜플마다 루트부터 leaf까지 탐색해야 함
뿐만 아니라 분할이 자주 발생해서 많은 페이지들을 수정해야 한다
또한 메모리에 불러온 페이지를 재사용하지 못해 캐시 효율이 낮아질 수 있다
정렬한 다음에 추가하기
대량의 데이터를 일단 정렬해준다.
-> 여기서 페이지단위로 그냥 잘라줌!! (즉 내가 원하는 채움비율을 맞출 수 있음)
그리고 이걸 그대로 leaf node로 활용한다.
=> 내부 노드 (부모노드)를 업데이트 해주기만 하면 된다.
또한.. 작은것부터 큰것순서로 넣기 떄문에 한번 분할이 일어나면, 더이상 왼쪽 노드랑은 상호작용을 하지 않는다
== 오른쪽은 새로운 페이지가 삽입될 때 계속 사용되므로 캐시에 올려서 효율적인 캐시활용이 가능하다!
(I/O가 적음)
뿐만 아니라 결과적으로 모든 리프페이지가 디스크에서 순차적으로 배치된다
나중에 쿼리 처리과정에서 도움이 된다
'학교 > 데이터베이스시스템응용' 카테고리의 다른 글
| 16. 11장 : HASH-BASEDINDEXING (0) | 2024.11.25 |
|---|---|
| 15. 10장 : TREE-STRUCTURED INDEXING (2) (0) | 2024.11.25 |
| 13. 9장 : STORING DATA - DISKS AND FILES (3) (0) | 2024.11.25 |
| 12. 9장 : STORING DATA - DISKS AND FILES (2) (0) | 2024.11.22 |
| 11. 9장 : STORING DATA - DISKS AND FILES (1) | 2024.11.21 |




