고정 헤더 영역
상세 컨텐츠
본문
앞에서 배운 B+ tree, ISAM이랑은 다르게 Hash index를 기반으로 한다
=> range 검색이 안된다!! equality 검색만 가능함
Static hasing -> ISAM같은 느낌
dynamic hashing -> B+ tree같은 느낌
...이렇게 두개를 비교해본다고 한다.
Static Hashing
해시함수를 이용해 데이터를 저장할 버킷을 결정한다 (h(k) mod M)
=> 이 때 M개의 버킷은 이미 할당되어 있는 페이지임!! (primary page)
=> 만약에 여러개의 데이터가 똑같은 버킷에 계속 담겨서 버킷이 가득찼다면..?
오버플로 페이지에 넘친걸 담아주고, 연결리스트 형태로 연결해준다.
장점 : 구현이 단순, 빠른 접근이 가능함 (해시함수를 이용하면 한번에 접근가능)
단점 : M을 너무 크게 설정하면 공간낭비 발생 가능, 오버플로가 많이 발생하면 연결리스트를 계속 타고타고 가야해서 빠른접근이 불가능 (디스크 I/O가 자주 발생하는것) <- long overflow chain이 생겼다구 한다!
long overflow chain은 데이터 조회, 삽입, 삭제에 모두 안좋은 영향을 준다.
Extendible Hashing
dynamic hashing중 하나. long oveflow chain 문제를 해결해준다!
=> bucket이 가득 찼을 때, 단순히 버킷 사이즈를 늘리는것으로는 해결이 불가능함 (모든 페이지에 대한 I/O를 해야함)
!! 버켓 포인터 디렉토리를 이용하자!
-> 버킷이 가득 찼을 때, 전체 파일을 재구성하는게 아니라 디렉터리 크기를 증가시켜서 해당 버킷만 분할시킨다.
가득차면...
1. 디렉터리의 크기를 두배로 늘림
2. 오버플로가 발생한 버킷만 새로운 버킷으로 분할함 -> 해싱함수의 새로운값에 맞게 분배
3. 해싱함수 조정 (늘어난 디렉토리 깊이에 맞추기)
디렉토리의 깊이를 d라고 하면,, 디렉토리의 크기는 $2^d$ 가 된다. (d가 2면, 디렉토리 크기는 4가되는것)
* 디렉토리 번호를 bit로 생각하면 된다!!
예시로 확인해보자!

이런 초기상태를 가진 디렉토리가 있다고 가정하자. global depth는 local depth의 max값이고
local depth는 mon n 의 n을 결정한다.
버켓마다 4개의 데이터가 들어가있으므로 local depth는 2가 된다.
hashing함수의 결과가 20인 데이터가 들어오면 어떻게 될까..?
-> 일단 global depth로 나눈 나머지를 확인해본다! (mod 4)
0이르모 bucket A에 담으려고 하는데.. 꽉차있어서 split을 수행한다.
일단 새로운 버켓을 하나 만들고, 버켓A와 new버켓의 local depth를 3으로 변경해준다.
이렇게 되면 -> 나머지가 00이었던 애들을 받아오는 버켓에서 각각 000 100 을 받아오는 버켓으로 변하게 된다.
즉 버켓 A와 새로운 데이터 20에 있는것들만 새로운 버켓 기준으로 넣어준다.
디렉토리에도 변화가 생긴다. locak depth가 증가했으므로 global depth또한 증가하게 된다. (3으로)
그러면 디렉토리 또한 8칸으로 증가하게 된다. 이 때 split되지 않는 나머지 버켓들에 대해서는, 그대로 유지된다
(같은곳을 포인팅하도록)

이렇게 변하게 된다.
=> 나머지 버킷에 대해서는 포인터만 복사해주면 되기 떄문에 부담이 적다!
Disk Access Efficiency
보통 디렉토리는 메모리에 올라가는 사이즈이다 -> 버킷탐색할 때 메모리에서 찾은 다음에 디스크로 한번만 접근하면 된다.
데이터 삭제 후 버킷이 비게되면, 두개의 버킷을 합쳐줄 수 있다. (split image 버킷과)
-> 이 때 병합 후 모든 항목이 동일한 버킷을 가리키면, 디렉토리 크기를 절반으로 줄일 수 있다.
단점 : 해시함수를 잘 안만들면, 하나의 버킷에 데이터가 집중될 수 있다. (의미없이 디렉토리만 냅다 커질 수 있음)
특히 중복이 많을 때 디렉토리가 커진다.
Linear Hashing
디렉토리를 사용하지 않는 동적 해싱 기법이다.
아이디어 : 여러개의 해시함수를 사용함 (h0, h1, h2....)
$h_i(\text{key}) = h(\text{key}) \mod (2^i N)$
* N : 초기 버킷 수
=> 각 단계마다 (i마다) 버킷의 범위가 증가한다.
일단 버킷이 가득차면 오버플로 페이지를 생성해서 데이터를 저장한다.
-> 오버플로가 발생한 페이지만 분할하는게 아니라, 버킷0부터 끝까지 순차적으로 분할한다.
버킷 분할은 라운드 단위로 이루어진다. (라운드 R에는 $2^R \cdot N$개의 버킷이 포함됨 (N은 초기버킷개수))
* 지금 라운드의 번호를 level이라고 한다....-> level에 따라 hashing 함수가 달라지는것!

이렇게 원래 이렇게 생긴 버킷이 있었다고 생각해보자...
내가오버플로! 라고 적어둔곳이 삽입때문에 오버플로가 필요해진 상황이라고 하면
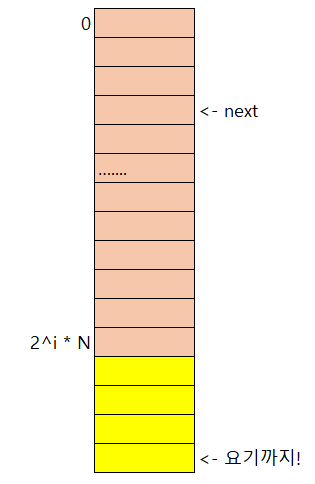
위에서부터, 오버플로가 발생한곳까지 늘려준다!
즉 라운드는 1 증가했고 (레벨이 1 증가함), next값은 저 오버플로가 발생했던곳이다.
그러면 나중에 search를 할 때...

해시함수를 써봤는데 갈색부분이다?! 그러면 노란색 부분까지 (split된부분) 확인해볼 필요가 있고
연갈색 부분 (빨간색으로 표시한 만큼, split이 안된부분) 이면, 그냥 저기서 찾으면 된다는것이다.
linear hashing의 경우, overflow 페이지가 생겼을때 바로바로 split을 진행하지 않는다.
oveflow 페이지를 유지해 두는데, 너무 길어졌을 때 split을 해준다고 한다.
-> 즉 필요없는데 split 되어서 공간차지만 하는걸, split 발생시점을 적절히 조절해서 방지할 수 있음
시간복잡도를 비교해보
| Heap File | Sorted File | Clustered Index | Hash Index | |
| Scan all records | $B \cdot D$ | $B \cdot D$ | $1.5 \cdot B \cdot D$ | $B \cdot D$ |
| Equality Search | $\frac{2}{b} \cdot D$ | $\log_2 B \cdot D$ | $\left(\log_F (1.5 \cdot B) + 1\right) \cdot D$ | $2 \cdot D$ |
| Range Serch | $B \cdot D$ | $\log_2 B \cdot D + pages \cdot D$ | $\left(\log_F (1.5 \cdot B) + pages\right) \cdot D$ | $B \cdot D$ |
| Insert | $2 \cdot D$ | $\log_2 B \cdot D + B \cdot D $ | $\left(\log_F (1.5 \cdot B) + 2\right) \cdot D$ | $3 \cdot D$ |
| Delete | $(\frac{2}{b} + 1) \cdot D$ | $\log_2 B \cdot D + B \cdot D $ | $\left(\log_F (1.5 \cdot B) + 2\right) \cdot D$ | $3 \cdot D$ |
- scan all record : hash index를 쓰지 말고, 그냥 파일 스캔을 이용하는게 낫다
- equality search : 해시테이블로 한번 접근 (key찾기) + key찾아서 힙파일접근 -> 총 2번만 디스크 I/O가 생긴다
- Range search : 해시 index를 이용할 수 없으므로 DB전체를 스캔한다
- Insert, Delete : 원하는 페이지를 찾는것에 2D (equality search) + 수정한 페이지를 다시 디스크로 옮기는것
| Heap File | Sorted File | Clustered Index | ||
| Scan all records | $O(B)$ | $O(B)$ | $O(B)$ | $O(B)$ |
| Equality Search | $O(B)$ | $O(\log_2 B)$ | $O(\log_F B)$ | $O(1)$ |
| Range Serch | $O(B)$ | $O(\log_2 B + pages)$ | $O(\log_F B + pages)$ | $O(B)$ |
| Insert | $O(1)$ | $O(B)$ | $O(\log_F B)$ | $O(1)$ |
| Delete | $O(B)$ | $O(B)$ | $O(\log_F B)$ | $O(1)$ |
'학교 > 데이터베이스시스템응용' 카테고리의 다른 글
| 18. 13장 : EXTERNAL SORTING (1) - Streaming (1) | 2024.12.18 |
|---|---|
| 17. 12장 : OVERVIEW OF QUERY EVALUATION (0) | 2024.12.17 |
| 15. 10장 : TREE-STRUCTURED INDEXING (2) (0) | 2024.11.25 |
| 14. 10장 : TREE-STRUCTURED INDEXING (1) (0) | 2024.11.25 |
| 13. 9장 : STORING DATA - DISKS AND FILES (3) (0) | 2024.11.25 |




