고정 헤더 영역
상세 컨텐츠
본문
예제를 가지고, 각 query plan의 cost를 생각해보자!
Reserves (sid: integer, bid: integer, day: date, rname: text)
each tuple : 40 bytes
한 페이지에 100 tuples
1000 pages
boat는 100가지 종류
Sailors (sid: integer, sname: text, rating: integer, age: real)
each tuple : 50 bytes
한 페이지에 80 tuples
500 pages
rating은 10종류
join을 위해 5page 사용가능
SELECT S.sname
FROM Reserves R, Sailors S
WHERE R.sid=S.sid
AND R.bid=100
AND S.rating>5;
Plan 1
- page nested loops를 사용한다.

S, R 순서니까
cost = [S] + [S] * [R] = 500 + 500 * 1000 = 500500 I/O
Plan 2
- select는 join의아래로 내릴 수 있음!!
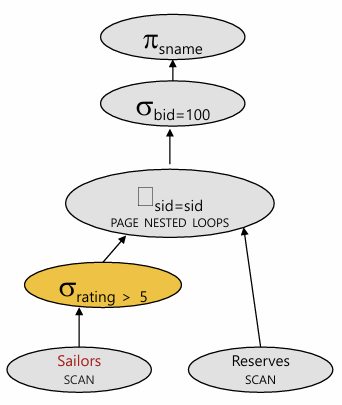
R이랑 join하는순간에, S의 page개수가 줄어든다. rating 범위가 10이라고 했으니까 대충 절만정도 날라갔다고 생각하면...
cost = 500 + 250 * 1000 = 250500 I/O
plan 3
- select가 위에 또있음!! 또 내려준다

각각의 salior에 맞게, 어쨌든 reserves를 스캔하긴 해야한다 (조건에 거르는건 나중문제)
cost = 500 + 250 * 1000 = 250500 I/O
plan 4
- join의 순서를 바꾸어 보자

R, S 순서로 바뀌었다!!
즉 [R] + [R] * [S] 로 생각을 해보면,,,
R 조건을 거르는게 유효해진다. 100종류의 보트종류가 있다고 했으니까 대충 1000/100 해서 10개로 줄어들게 된다.
cost = 1000 + 10 * 500 = 6000 I/O
plan 5
- s에서 rating > 5 도 유의미하게 만들고싶다 -> materializing

rating > 5를 뽑아서, 디스크에 sub table로 저장한다. (여기서는 250개의 페이지를 가지는 테이블이 될것)
그리고 join을 할 때 이 sub table을 이용해준다,
-> 즉 곱하기할 때 사용하는게 sub table의 I/O이고, sub table을 디스크에 작성하는 I/O를 추가해준다.
R, S를 각각 한번씩 읽는것
하나의 R에 대해, S를 반복할건데,,,, 이걸 sub table로 바꿈! sub table을 저장하는 I/O 250
반복하는 R 페이지 개수가 10으로 줄어들었음
각 R에 대해, sub table을 스캔해옴 (10 * 250)
cost = 1000 + 500 + 250 + 10 * 250 = 4250 I/O
plan 6
- join 순서를 또 바꾸어보자

S, R 순서인것 주의
R, S를 각각 한번씩 읽는것
R의 sub table을 저장함 (10 페이지)
S또한 250으로 줄었음
각 S에 대해, sub table을 스캔해옴 (250 * 10)
cost = 500 + 1000 + 10 + 250 * 10 = 4010 I/O
plan 7
- join 알고리즘을 바꿔보자!

Sort Merge Join으로 변경!
join을 위한 5 페이지가 있다고 했으니까.... B = 5
S, R을 각각 한번씩 읽는것
S, R을 정렬하는것 -> 이 때, 각각 select 기준이 적용된채로 input이 들어온다! (즉 sort의 pass0은 select에서 바로 올라옴)
R을 정렬하기 위해 앞에서 배운 2 way sort 알고리즘을 사용한다. (10개의 페이지가 input으로)
Pass 0 : 읽어오는건 이미 했으니까, write만 한번 -> 10
그리고 버퍼 5개를 이용해 RUN을 만드니까 총 2개의 RUN이 생긴다
Pass 1 : RUN을 읽어오고, 결과를 write한다 -> 20
이 때, RUN이 2개였으니까 pass 1에서 결과가 나온다
S를 정렬하기 위해 (250개의 페이지가 input으로)
pass 0 : write만 -> 250
버퍼 5개로, RUN 50개를 만든다
pass 1 : read, write -> 500
입력버퍼 4개, 출력버퍼1개, 총 50/4 = 13개의 RUN이 생긴다
pass 2 : read, write -> 500
13 / 4 = 4개의 RUN이 생긴다
pass 3 : read, write -> 500
4 / 4 = 1개의 RUN이 생긴다 == 정렬 마무리!
정렬한 다음에 merge하는것 -> [정렬S] + [정렬R] = 250 + 10
cost = 1000 + 500 + sort R (10 + 2 * 10) + sort S(250 * 2 * 3 * 250) + 250 + 10 = 3540
plan 8
- materializing 을 적용해보자

각각의 sub table을 디스크에 저장하고
각 정렬의 pass 0 에서 디스크에서 read해오는 동작이 추가된다.
cost = 1000 + 500 + sub table(10 + 250) + sort R (20 + 2 * 10) + sort S(500 * 2 * 3 * 250) + 250 + 10 = 4060
plan 9
- Block nested loop로 join을 변경해보자 (chunk!!)

B-2만큼씩 묶어서 루프를 돌린다 (특정 청크당 한번씩 페이지 불러오기)
S, R 순서니까 S를 B-2 (여기서는 3)으로 나눠준다.
S, R 가져오기
R의 sub table 저장하기 (10)
S의 청크단위로 sub table 불러오기 ( 250/3 * 10)
cost = 500 + 1000 + 10 + (84 * 10) = 2350 I/O
plan 11
- projection도 아래로 내릴 수 있다!

mat이 없어진 이유 : sid만 잘라서 가져왔으니까, 테이블 크기 자체가 엄청 작아짐!! (10분의 1로 줄어든다) 굳이 필요없어서 뺐다
R을 가져오는것 1000
R에서 bid = 100인것만 선택하면, 10 페이지만큼의 분량을 차지한다.
여기서 또 sid만! 빼오면,, 하나의 튜플의 크기가 10분의 1로 줄어드므로,, 전체 크기가 한페이지밖에 안된다.
즉 R 자체를 버퍼에 계속 올려둘 수 있게된다.
- 그러니까 그냥 S를 한번 스캔해서 바로바로 버퍼에 있는 R에 적용해주면 된다 == 1 * 500
cost = 1000 + 1 * 500 = 1500
index
파일이 indexing 되어있다면 어떻게 될까 (index nested loop를 사용한다)
R.bid clustered
S.sid unclustered : 하지만 sid가 primary key여서, 튜플 한개씩만 존재함 (==페이지 한개만 가져옴)
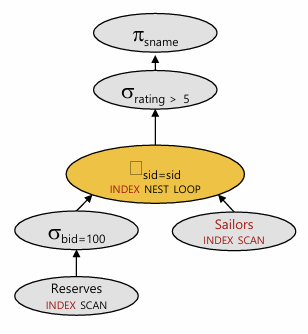
R을 index scan으로 가져올 수 있다!! clustered 되어있으므로,, bid = 100을 찾아서 연속해서 10페이지만 가져오면된다. (10)
R의 한페이지에 100개의 튜플이 들어가니까,, 총 1000개의 튜플이 존재한다.
이 각 R 튜플에 대해 S에서 INDEX Search를 진행한다 (한번에 1 I/O)
cost = 10 + 1 * 1000 = 1010 I/O
'학교 > 데이터베이스시스템응용' 카테고리의 다른 글
| 28. 15장 : A TYPICAL RELATIONAL QUERY OPTIMIZER (3) (1) | 2024.12.19 |
|---|---|
| 26. 15장 : A TYPICAL RELATIONAL QUERY OPTIMIZER (1) (0) | 2024.12.19 |
| 24. 14장 : EVALUATING RELATIONAL OPERATORS (2) - Sort Merge Join (0) | 2024.12.19 |
| 23. 14장 : EVALUATING RELATIONAL OPERATORS (1) - Nested Loops Join (0) | 2024.12.19 |
| 22. 13장 : EXTERNAL SORTING (5) - 병렬처리 (0) | 2024.12.19 |




